Introduction: C'est Reynolds, un ingénieur anglais spécialiste
de l'hydrodynamique qui a introduit ce nombre qui porte son nom et qui
est constamment utilisé dans les calculs. Il est fonction de trois
paramètres : La corde de l'aile "l", la vitesse relative "V" de
l'avion par rapport à l'air et de la viscosité cinématique
du fluide "n".
V en m/s (1m/s = 3,6 km/h)
l en m
n en m²/s
Tant que les conditions atmosphériques sont normales, la viscosité
cinématique du fluide reste constante égale à 0,0000145m²/s
Exemples:
Un planeur à une largeur d'aile
constante égale à 23 cm et vole à 40 km/h ;quel est
le nombre de Reynolds correspondant ?
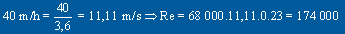
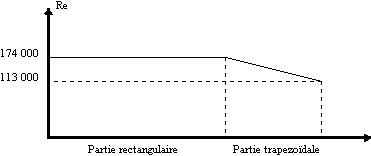
‚Un planeur a une aile à extrémités
trapézoïdales dont les dimensions sont données (Fig.1);
la vitesse est de 40 km/h, calculer la répartition des nombres de
Reynolds le long de l'envergure.
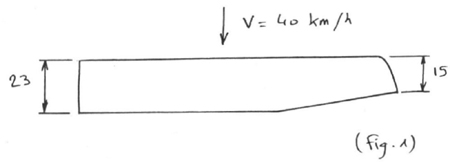
La corde variant le long de l'aile, le nombre de Reynolds ne sera pas
constant sur toute l'aile; il sera constant sur la partie rectangulaire
et variera linéairement le long de la partie trapézoïdale.
nombre de Reynolds sur la partie rectangulaire:
Re =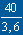 
x 68 000 x 0,23 = 174 000
nombre de Reynolds au niveau du bord marginal:
Re =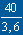
x 68 000 x 0,15 = 113 000
Répartition le long de l'aile:
Influence du nombre de Reynolds sur les caractéristiques
Introduction: le nombre de Reynolds étant proportionnel
à la vitesse et à la corde de l'aile, on voit que nos modèles
réduits volent à des nombres de Reynolds beaucoup plus faibles
que les planeurs grandeur.
On peut voir des ordres de grandeurs dans le tableau ci-dessous:
| Corde (m) |
Vitesse (m/s) |
Nombre de Reynolds |
Type d'appareil |
| 0,25 |
15 |
250 000
|
avion modèle réduit |
| 1,50 |
25
|
2 500 000
|
avion réel genre Rallye |
| 0,24 |
12
|
198 000
|
emplanture de 4m modèle réduit |
| 0,10 |
12
|
82 000
|
saumon de 4 m modèle réduit |
| 1,00 |
25
|
1 720 000
|
emplanture vrai planeur |
| 0,40 |
25
|
689 000
|
saumon vrai planeur |
Pourtant certains profils sont utilisés aussi bien en modélisme
qu'en aviation grandeur (NACA, BERTIN, WORTMANN...). Leurs caractéristiques
varient sensiblement lorsque le nombre de Reynolds change (lorsque
Re ø, Cz ø
par exemple).
Pour cette raison, les polaires disponibles concernant ces profils
ne sont pas toujours utilisables pour les modèles réduits
car elles ont été tracées à des Re de
plusieurs millions qui caractérisent le vol grandeur.
Il faut donc se méfier et bien vérifier que les polaires
sur lesquelles vous prélevez des valeurs sont tracées à
des nombres de Reynolds correspondant bien aux vitesses de vol de votre
planeur.
On ne connaît que peu de mesures effectuées en soufflerie
pour les petits nombres de Reynolds (10 000 < Re < 100 000). Dans
ce domaine, les coefficients aérodynamiques des profils sont fortement
dépendants du nombre de Reynolds et, donc, jusqu'à présent
ne peuvent être déterminés qu'expérimentalement.
Dans les applications techniques, ces nombres de Reynolds se présentent
dans le cas de petits ventilateurs ou à régime lent (climatisation),
de compresseurs et de turbines de réacteurs à grande altitude,
dans la partie de basse pression de turbine à vapeur, et, ce n'est
pas le moindre domaine, dans le modélisme aujourd'hui très
développé. En général, on utilise des profils
qui en réalité ont été conçus et mesurés
pour des nombres de Reynolds plus importants. En outre, il existe toute
une série de profils calculés théoriquement. Pour
permettre une possibilité de comparaison des performances de ces
profils dans le domaine des nombres de Reynolds critiques, des mesures
polaires sur une série de profils ont été effectués
dans la soufflerie de l'Institut d'Aérodynamique de l'Université
de Stuttgart et sont rassemblées dans le recueil "Profilpolaren
für den Modellflug" de Dieter Althaus paru aux éditions Neckar.
Dans cet ouvrage figurent les polaires, coordonnées et silhouettes
de quelques 45 profils usuels, ce qui permet d'effectuer des comparaisons
sérieuses; en effet, il ne faut pas comparer les caractéristiques
de profils extraites de polaires prises ici et là dans la littérature
modéliste car ces polaires n'ont pas toutes été tracées
à partir d'essais effectués dans une même soufflerie,
comme c'est le cas pour le recueil cité plus haut, ce qui est gênant
car aux faibles nombres de Reynolds, certaines souffleries donnent des
résultats très approximatifs; le recueil cité plus
haut, étant donnée la vaste étude effectuée
dans la seule soufflerie de Stuttgart est l'ouvrage à posséder
pour pouvoir choisir un profil correctement.
Influence du nombre de Reynolds sur Cz maxi :
On voit sur la (fig.2) l'influence du nombre de Reynolds sur le Cz maxi
des profils Clark Y, NACA 0012, Eppler 205, NACA 23012, NACA 4412, Göttingen
796 et 623.
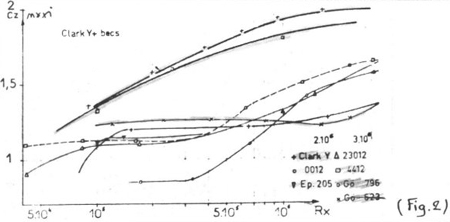
On constate donc que les caractéristiques de portances s'améliorent
avec le nombre de Reynolds. On constaterait de même en traçant
les courbes (
)mini
(finesse mini) et (
)mini
(vitesse de chute mini) en fonction du nombre de Reynolds que la finesse
s'améliore et que la vitesse de chute diminue si l'on augmente le
nombre de Reynolds.
On pourrait donc croire qu'il faut voler au plus grand nombre de Reynolds
possible en augmentant la corde de l'aile ou la vitesse de vol; mais en
fait, alors que les caractéristiques du profil s'améliorent
en augmentant Re, celles de l'aile ne suivent pas les mêmes
variations à cause des phénomènes d'écoulement
autour de l'aile pour lesquels l'augmentation du nombre de Reynolds par
augmentation de la corde par exemple peu être néfaste (voir
à ce sujet le chapitre sur l'allongement).
Le nombre de Reynolds critique:
En dessous d'une certaine valeur du nombre de Reynolds, le coefficient
de résistance d'un corps augmente soudain considérablement,
alors que le coefficient de portance diminue très rapidement. Pour
les profils d'ailes, cela se traduit par une diminution brutale des performances;
ceci peut être visualisé sur le diagramme qui en (Fig.3) représente
le rapport ()maxi
qui traduit la finesse maxi du profil en fonction du nombre de Reynolds.
Cette chute des caractéristiques est très visible en
particulier sur la courbe du profil FX-M2 en dessous d'une valeur de Re=80
000 qui sera donc le nombre de Reynolds critique pour ce profil.
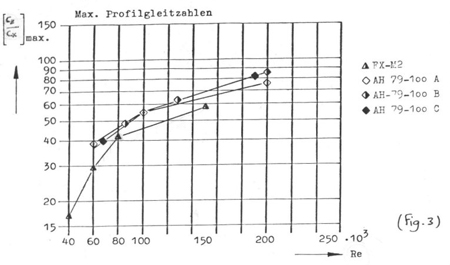
On comprend que lorsqu'une aile vole à Rec (nombre de Reynolds
critique) ou en dessous, ses performances sont nettement diminuées.
Le Rec varie pour chaque profil et est fonction de la forme du profil
mais surtout de son épaisseur relative. Plus l'épaisseur
relative du profil est importante, plus le Rec est grand, donc plus il
faudra voler vite ou agrandir la corde (le nombre de Reynolds leur est
proportionnel) pour voler au dessus de Rec.
A cause de Rec, on recommande souvent une corde d'aile minimale en
fonction de la vitesse de vol moyenne du modèle. Ceci permet de
se situer au dessus de Rec et d'éviter tous ces problèmes
et de conserver des bonnes performances pour le modèle.
Le Rec peut influer sur le choix d'un profil : on ne mettra pas un
profil ayant un Rec élevé sur un planeur thermique qui doit
parfois voler lentement.
On constate que le profil type plaque creuse est supérieur pour
de faible valeurs de Re (voir Fig.4).
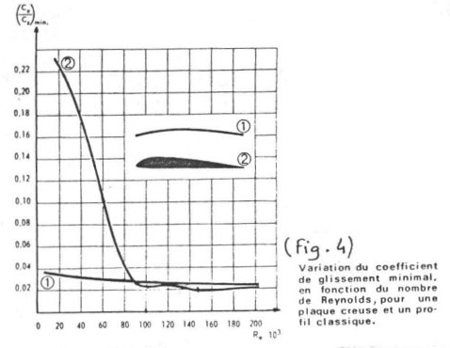
Ceci est dû au fait que le bord vif à l'avant produit une
turbulence dans la couche limite ce qui évite le décollement
prématuré de celle-ci.
Il est possible d'introduire de semblables perturbations sur nos modèles
pour adapter nos profils aux faibles nombres de Reynolds. C'est ce qui
à été réalisé depuis longtemps en vol
libre grâce à l'emploi de "turbulateurs" dont il existe deux
types de base:
-
Le premier est le fil dit de "préturbulence" placé à
l'avant du bord d'attaque; il rend l'écoulement libre turbulent
lequel crée à son tour une turbulence dans la couche limite.
-
Le deuxième procédé consiste à rendre instable
la couche limite elle-même par différents moyens : rugosité
de surface(par exemple, papier abrasif collé à proximité
du bord d'attaque sur l'extrados), fil collé avant le point de transition
et perturbant la couche limite, donnant assez d'énergie cinétique
aux particules d'air pour ne pas être aspirées par la dépression
de l'extrados, provoquant ainsi le décollement de la couche limite.
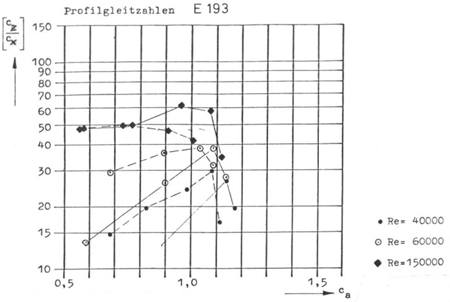
C'est ce qui à été expérimenté dans
le cas de la (Fig.5) où l'on voit des polaires caractérisant
l'Eppler 193 avec ou sans turbulateur (respectivement courbes en traits
continus et courbes en traits discontinus) à différents Re.
Le nombre de Reynolds critique de ce profil es t approximativement
Rec = 100 000 et on voit que, pour des nombres de Re inférieurs
à 100 000 (ici pour 60 000 et 80 000), les caractéristiques
sont supérieures avec turbulateur.
Au dessus de 100 000 (ici 150 000), le turbulateur est nuisible.
Remarque: la couche turbulente trouve une nouvelle application
pour de plus grands nombres de Reynolds pour l'emploi de volets de courbure
en empêchant le décollement de la couche limite à proximité
de l'angle dièdre produit par la déflexion du volet.
