Définition :
L'allongement l est facile à
définir sur une aile rectangulaire : c'est le rapport de
l'envergure E sur la corde C :
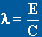
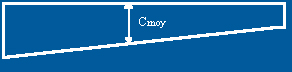
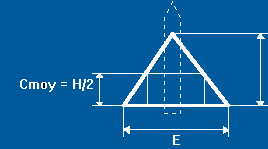
Pour une aile trapézoïdale, c'est le rapport de
l'envergure E sur la corde moyenne Cmoy
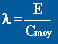
Pour une aile D on ne peut pas le
définir de cette façon; on le définit comme
étant le rapport du carré de l'envergure par la surface
de l'aile :
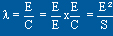
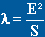
Remarques :
- Pour la surface S on tient aussi compte de la partie de l'aile
cachée par le fuselage.
- La surface alaire exclut les surfaces des gouvernes de
profondeur car celles-ci ne portent pas, elles stabilisent.
De plus, cette formule est valable pour toutes les formes d'ailes,
réciproquement, on peut définir la corde moyenne comme
le rapport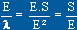 
, ce qui permet de la situer, cela peut être utile
par la suite (par exemple pour centre l'appareil; en effet, le
centrage doit s'effectuer en connaissance du centre de poussée
qui est sur cette corde moyenne).
Exemple :
Lors de l'écoulement de l'air autour d'une aile, dont
l'angle d'attaque est a, il se produit
autour du profil, par l'effet de la viscosité, une circulation
qui donne naissance à une force perpendiculaire à
l'écoulement libre et appelée portance.
Pour une aile d'envergure E, la circulation et donc la portance
varient le long de cette aile; d'après la loi de Prandtl, la
force de tourbillon totale est constante et l'on en déduit que
des lignes de tourbillons s'écartent de l'aile; celle-ci se
dirigent vers l'arrière et rejoignent les lignes
d'écoulement derrière l'aile; elles provoquent un champ
de vitesse incliné vers le bas. De ce fait, l'aile rencontre
l'écoulement sous un angle qui diffère de l'angle
d'attaque géométriquement, la différence
étant appelée angle induit. Cet angle se calcule
à partie de la formule :
La force élévatrice s'incline vers l'arrière
en donnant naissance à une composante dirigée dans le
sens de l'écoulement; celle-ci, équivalente à
une traînée (traînée induite) s'ajoute
à celle existant déjà (même dans un
écoulement sans frottements). La traînée induite
se calcule simplement :
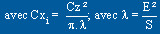
On voit donc que lorsque l'allongement augmente, la
traînée diminue; c'est pourquoi les planeurs modernes
grandeurs ont un allongement important (de l'ordre de 20 à 30)
afin de diminuer la traînée induite.
En modélisme, le problème est différent; en
effet nos planeurs évoluant à des Re proches du Rec (Re
critique) au dessous duquel les caractéristiques des profils
chutent en catastrophe. Si, pour une envergure donnée, on
augmente l'allongement (donc on diminue les cordes) pour obtenir une
traînée induite plus faible, on risque de faire
évoluer dans un Re subcritique avec toutes les
conséquences néfastes que cela implique; de toute
façon, lorsqu'on augmente l
même si l'on atteint pas Rec, nos planeurs évoluent dans
des plages de Re plus faible, ce qui réduira les performances
des profils.
Ainsi, un gain de traînée induite résultant d'un
accroissement de l'allongement pourra être annulé par
l'augmentation de la traînée provoquée par la
diminution de Re, par la réduction de la corde. On peut
calculer l'influence de ces deux phénomènes d'effets
opposés pour savoir s'il est utile ou non d'augmenter
l'allongement, et trouver l'allongement optimum.
Exemple :
E 61, planeur de 2 m d'envergure.
Admettons que l'on veuille faire travailler ce profil à
finesse max.
On ne change pas la vitesse de vol que l'on fixe à 6 m/s (on
la suppose constante).
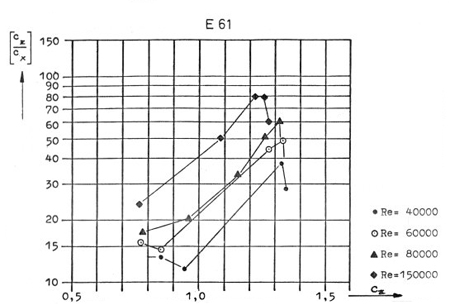
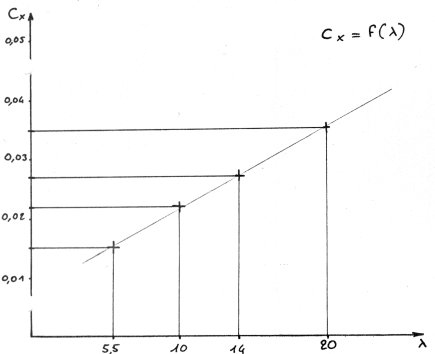
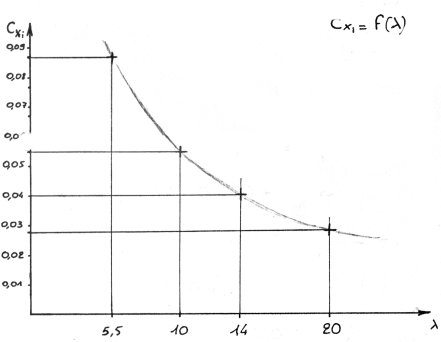
On peut tracer Cxi = f(l) puis Cx =
f(l), puis la courbe Cxi + Cx = f(l) dont le minimum nous donnera l'allongement
idéal.
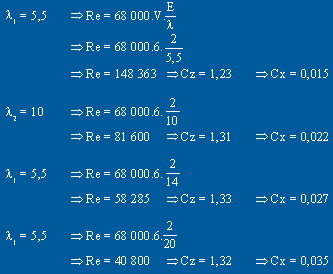
Commentaires :
A partir du Re on se reporte sur la courbe [
] = f (Cz) où on lit le Cz
à finesse max., puis on calcule le Cx à partir
du 
.
On utilise enfin la formule Cxi =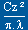 
pour
calculer le Cxi .
Calcul des Cxi :
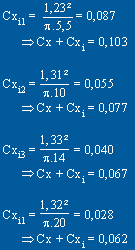
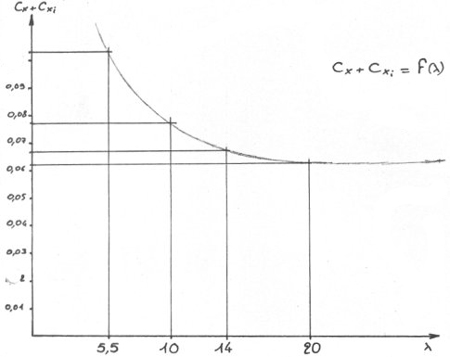
Cette courbe montre l'évolution du coefficient de
traînée de l'aile entière (Cx + Cxi :
coefficient de traînée de profil + coefficient de
traînée induite) ce dernier diminue quand l augmente. Afin de trouver l permettant de faire travailler l'aile à
finesse max., il est nécessaire de faire intervenir le
coefficient de portance Cz. La finesse max. de l'aile se traduira par
le rapport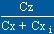 
max., nous allons donc tracer la courbe 
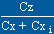= f (l)
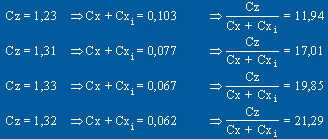
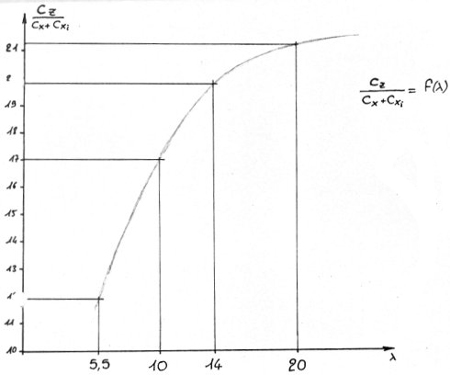
Théoriquement, d'après les courbes ainsi obtenues,
il faudrait donc faire un allongement le plus grand possible.
Toutefois ce raisonnement n'est valable que lorsque le planeur vole
à finesse max., ce qui n'est pas toujours le cas. Pour obtenir
l'allongement optimum dans un maximum de configuration de vol, il
faut faire un compromis et donc retracer la série de courbes
précédentes à partir d'un Cz (et donc d'un Cx)
différent. Pour choisir ces valeurs, on utilise la polaire du
profil.
Il faut cependant ne pas prendre des valeurs trop importante de l car pour une envergure donnée, cela
conduit à diminuer la corde, donc la surface et par
conséquent la force de portance de l'aile, car Rz force de
portance qui doit sustenter l'avion n'est pas seulement fonction de
Cz mais aussi de S : 
; Rz doit être égale au poids de l'avion;
ceci conduit à déterminer une surface mini, ce que nous
calculons avec la formule :
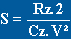avec
Rz = P
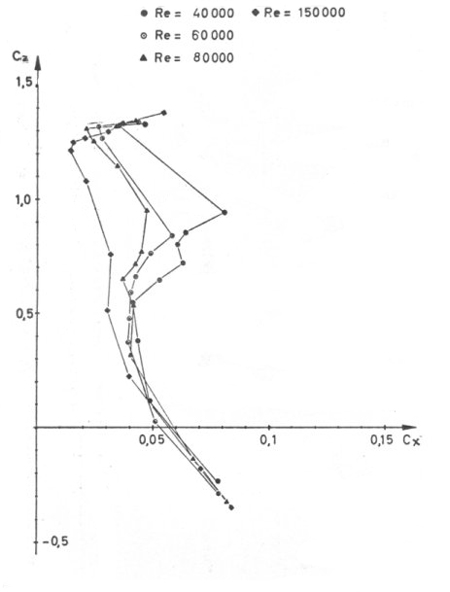
En effet , on s'aperçoit que dans la zone de Cz » 1, le Cx varie énormément
suivant le Re avec lequel on travaille. En fait, si l'on
traçait la courbe 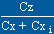= f (l),
nous obtiendrions une courbe qui aurait l'allure suivante :
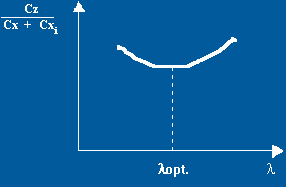
qui nous donnerait par lecture directe lopt. (l
optimum).
Une autre méthode de calcul consiste à prendre les
hypothèses suivantes :
- envergure donnée
- profil donné (2 essais E 193 - E 385)
- on se place en vitesse de chute mini; pour cela on utilise la
courbe
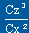= f (Cz), dont les résultats ont
été transformés en courbes [Vitesse de chute
(en m/s) = f (l)].
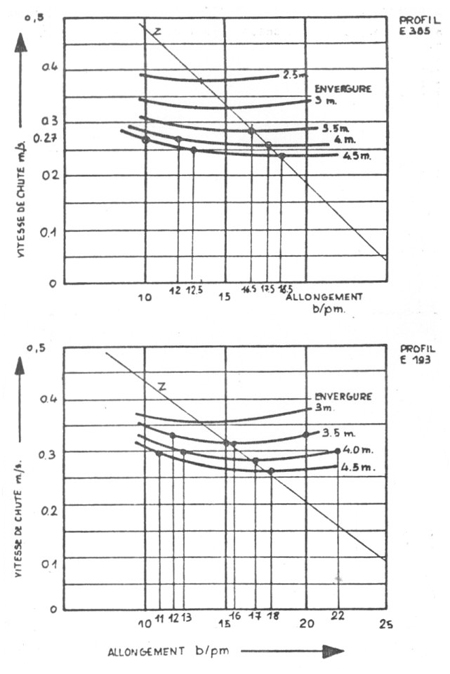
Conclusions, interprétation des résultats fournis
par l'étude :
- L'allongement optimal est obtenu pour les valeurs de l correspondant aux vitesses de chute les
plus basses. On remarque que l'on peut tracer unes droite passant
par tout ces points déterminés pour chaque
envergure.
- Mais on remarque que pour les petites envergures,
l'écart de performances varie peu si l'on s'écarte
de l'allongement optimum.
Exemple : première courbe, profil E 385
- planeur de 2,5 m d'envergure
L'allongement optimal est de 13 et correspond à une vitesse
de chute de 0,38 m/s
Un allongement de 10 à 17 n'augmente pas la vitesse de chute
de plus de 0,01 m/s (0,39 m/s), ce qui représente un
pourcentage de 2,6 %.
L'allongement optimal est de 15 et correspond à une vitesse
de chute de 0,32 m/s
Cette vitesse n'augmente pas plus que 0,01 m/s (0,33 m/s) pour des
allongements allant de 11 à 18, soit 3 %.
La courbe n'a plus une allure symétrique,
c'est-à-dire qu'il est plus néfaste de trop diminuer
l'allongement que de trop l'augmenter; en effet, l'allongement
devient plus important sur Cxi (traînée
induite) que sur Cx (traînée du profil).
L'allongement idéal est 17,5; si on diminue cet allongement
jusqu'à 12, on perd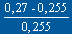 
= 6 % de performances en vitesse de
chute.
Ce pourcentage n'est encore pas très important pour une telle
diminution de l'allongement, et il faut se rendre compte que si on
reste dans une fourchette d'allongement comprise entre 15 et 20,
l'effet de l'allongement ne se fait pas sentir sur la vitesse de
chute, car il y a équilibre entre les 2
phénomènes opposés qui interviennent, à
savoir la variation de traînée induite et la variation
des performances du profil.
Remarques :
- Pour réduire la traînée induite, on peut
aussi agir sur la répartition de la portance le long de
l'aile; on montre en effet que lorsque la répartition de
portance est elliptique le long de l'envergure, la
traînée induite est minimale.
- Ces considérations de traînée ne doivent
pas être les seules à intervenir pour la
détermination de l'allongement; en effet, si pour une
envergure donnée, on augmente l'allongement, on
réduit la corde donc l'épaisseur de l'aile, donc sa
résistance et se posent alors les problèmes de
résistance à la flexion.
