Introduction : Les polaires sont des courbes permettant de déterminer
les caractéristiques d'un profil, d'une aile, d'un appareil. Elles
sont par exemple très utiles pour comparer les profils entre eux,
afin de choisir celui qui sera le mieux adapté à l'utilisation
qu'on désire en faire.
Remarques:
De nombreuses polaires
font intervenir le nombre de Reynolds; il faut bien faire attention à
ne comparer que des polaires réalisées à un même
nombre de Reynolds.
‚Les polaires des profils
permettent de les comparer entre eux plutôt que de définir
leurs performances exactes; en effet, elles n'ont pas toujours été
établies avec précision (maquettes peu précises, souffleries
non adaptées aux faibles vitesses de vol de nos planeurs et donc
à des essais à faibles vitesses d'écoulement de l'air,
polaires résultants de calculs à l'ordinateur...).
Polaire coefficient de portance en fonction du coefficient de
traînée : Cz = f (Cx)
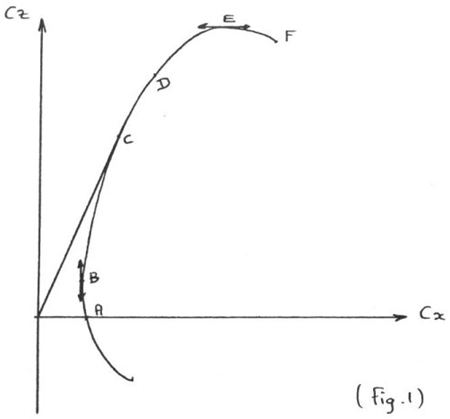
On peu d'abord déduire de cette polaire les points remarquables
suivants :
-
point A : point de portance nulle à l'intersection de la polaire
et de l'axe des Cx; il donne la traînée à portance
nulle.
-
point B : point de traînée minimale; déterminé
avec la tangente verticale à la courbe.
-
point C : point de finesse maxi, déterminé avec la tangente
à la courbe qui passe par l'origine; c'est le point pour lequel
on a le plus grand rapport
.
-
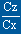point D : point de vitesse de chute minimale déterminé par
le calcul de
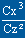mini.
-
point E : point de portance maximale, déterminé avec la tangente
horizontale à la courbe.
-
point F : point de décrochage.
La polaire Cz = f (Cx) représentée en (Fig.1) exprime
par exemple la variation de Cz en fonction de Cx (pour un nombre de Reynolds
donné car cette courbe se déplacerait si l'on faisait varier
le nombre de Reynolds). A partir de cette polaire, on peut obtenir la polaire
de l'aile équipée d'un tel profil. Si l'aile est rectangulaire,
le Cz ne change pas, c'est celui du profil; seul le Cx augmente d'une valeur
égale à la traînée induite résultant
du fait que l'aile n'a pas une envergure infinie et qu'il existe donc des
traînées marginales appelées traînées
induites.
Donc pour obtenir la polaire de l'aile, il suffit de déplacer
la polaire du profil vers les Cx croissants de la valeur Cxi.
On peut aussi obtenir la polaire du planeur complet en considérant
que le fuselage et son empennage n'apportent aucune portance supplémentaire
(les surfaces horizontales de l'empennage ne portent pas théoriquement
si l'avion est bien centré) mais seulement de la traînée
(traînée du fuseau + traînée des empennages +
traînées résultant des interactions, c'est-à-dire
des jonctions aile-fuselage et empennage-fuselage + traînées
"parasites" (fils d'antenne, cockpit...) ).
Donc pour obtenir la polaire du planeur complet à partir de
laquelle on pourra tenter de trouver des valeurs de finesse, de chute mini
..., il faut encore décaler la polaire de l'aile en lui ajoutant
toutes les traînées citées ci-dessus; ceci est représenté
en (Fig.2).
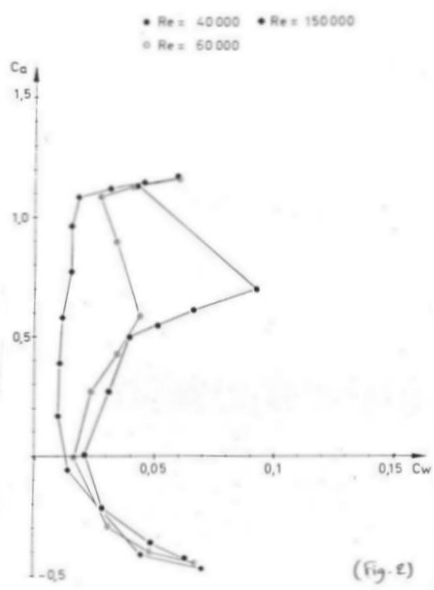
En général, on ne fournit pas une seule polaire mais une
famille de polaires tracées à des nombres de Reynolds différents.
(cf Fig.2), où on voit un exemple de polaires Cz (Cx) tracées
pour l'Eppler 193.
On voit que deux de ces polaires n'ont pas exactement la même
forme que celle qui est représentée en (Fig.1); ce sont les
deux polaires tracées à 40 000 et 60 000 Reynolds. Ceci est
dû à une traînée plus forte car le profil travaillait
en dessous de son nombre de Reynolds critique et ses caractéristiques
en sont fortement affectées.
A partir d'une famille de polaires tracées à plusieurs
nombres de Reynolds, on peut tracer d'autres courbes qui sont directement
exploitables pour la comparaison de deux profils. ce sont les courbes (
)
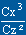fonction de Cz; (
)
fonction de Cz; (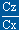
)maxi
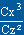fonction de Re; (
)
fonction de Re.
Les courbes (
)
fonction de Cz :
Elles permettent pour chaque nombre de Reynolds (donc pour chaque vitesse)
de déterminer le point de finesse maxi du profil, c'est-à-dire
la valeur de cette finesse maxi et la valeur du Cz lui correspondant (Fig.3).
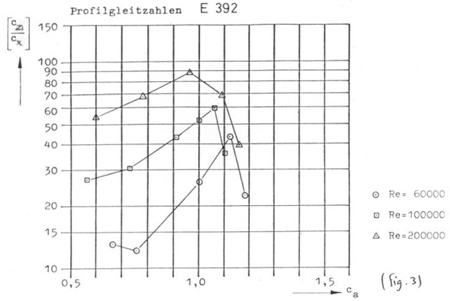
Les courbes (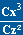
)
fonction de Cz :
Elles permettent de trouver le point de vitesse de chute mini et la
valeur du Cz correspondant à cette vitesse mini de chute (Fig.4).
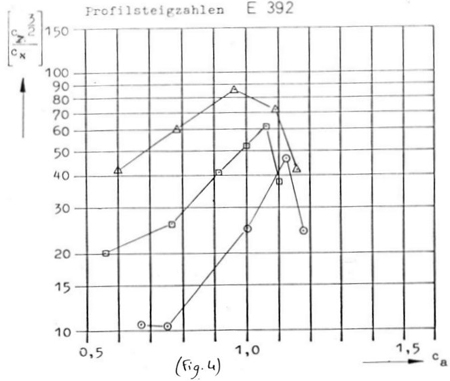
Remarque : on voit que les valeurs de Cz correspondant à la finesse
maxi sont très proches des valeurs correspondant à la vitesse
de chute mini (ceci en comparant les (Fig.3) et (Fig.4) ); c'est une constatation
classique en modèle réduit et il n'est généralement
pas utile de faire les deux calculs tant l'écart est faible.
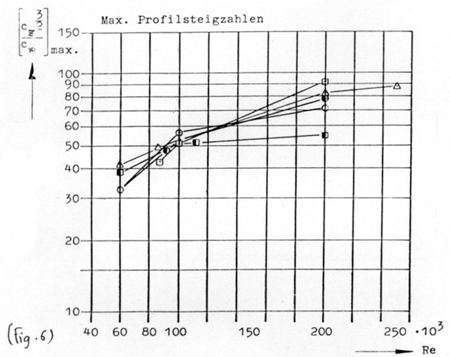
Les courbes ()maxi
fonction de Re :
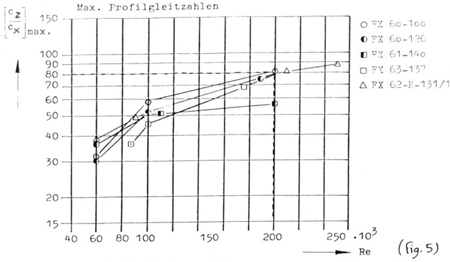
Ce sont les courbes qui permettent le mieux de comparer les profils
(dans le cas où on désire obtenir une finesse maximum); elles
sont de plus en plus souvent fournies pour plusieurs profils comme c'est
le cas en (Fig.5) où on peut voir ces courbes tracées pour
quelques profils Wortmann. On peut y constater par exemple que le profil
FX 60.100 est le plus fin au dessus de 100 000 Re mais que ses caractéristiques
changent et baissent en dessous de 100 000 Re; il ne faudra donc employer
ce profil que si l'on est sûr de voler à des Re supérieurs
à 100 000.
Les courbes (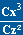)maxi
fonction de Re :
Elles permettent d'établir un classement des profils en considérant
cette fois leur vitesse de chute mini; on peut constater qu'au dessus de
125 000 Re, c'est le profil FX 63.137 qui chutera le moins, alors qu'aux
faibles nombres de Reynolds, on lui préférera le FX 62.K.131/17
Conclusion : l'observation de ces courbes permet de choisir le
profil le plus adapté à la conception du planeur. elle permet
aussi de trouver le point de fonctionnement du profil :
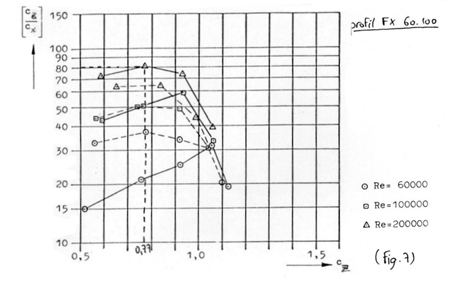
Exemple : le choix s'est porté sur le profil FX 60.100 car c'est
celui qui offre la meilleure finesse. Après avoir estimé
la vitesse du planeur, on connaît le nombre de Reynolds qui sera
de 200 000; on en déduit sa finesse maxi : 80, on reporte ce nombre
sur la courbe ()
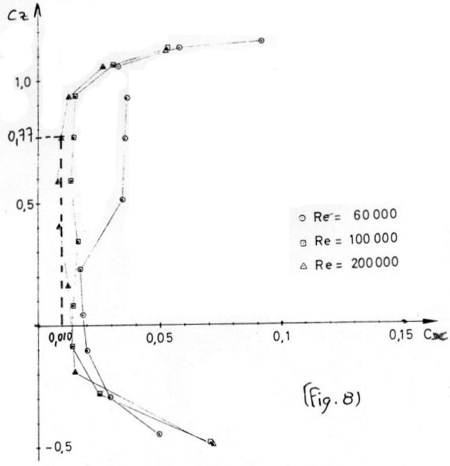
fonction de Cz (Fig.7) et on obtient Cz = 0,77. Ce nombre reporté
sur la (Fig.8) permet de déterminer Cx = 0,010 (Attention, pour
ces deux dernières déterminations, il faut bien prendre la
courbe à Re = 200 000).
Une fois que l'on a déterminé le nombre de Reynolds auquel
le profil va évoluer, sa finesse, son Cz, son Cx, on peut déterminer
l'angle d'incidence grâce à la courbe Cz fonction de a
(angle d'incidence); ceci permettra par exemple de calculer l'angle de
calage de l'aile sur le fuselage.
Donc, la détermination de l'angle d'incidence à partir
du Cz est une des utilisations des...
...Courbes Cz fonction de l'incidence a
:
ces courbes représentent l'évolution du Cz du profil
en fonction de l'angle d'incidence. Elles ont l'allure représentée
en (Fig.9):
-
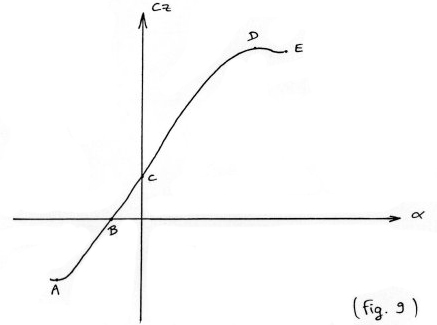
point A :le profil a une portance négative (cas du vol dos par exemple)
entre les points A et B; ceci signifie qu'il y a une pression à
l'extrados et une dépression à l'intrados; au point A, on
est au minimum de portance, c'est-à-dire à la portance négative
maximale.
-
point B : c'est le point correspondant à la portance nulle;
L'angle correspondant à la portance nulle est souvent noté
Io ou b.
-
point C : point d'incidence nulle : la vitesse de l'aile par rapport à
l'air qui l'environne est parallèle à la corde du profil.
Permet de connaître Cz à incidence nulle.
-
point D : point de portance maxi; si l'on augmente l'incidence au delà
de la valeur obtenue pour ce point, le phénomène de décrochage
apparaît et le Cz chute.
Exemple:
La polaire de la (Fig.10) représente la variation de Cz en fonction
de l'angle d'incidence pour le profil FX 60.100; on voit que les trois
courbes tracées à trois nombres de Reynolds différents
sont relativement similaires.
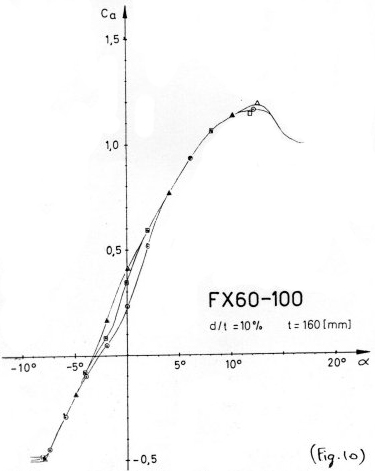
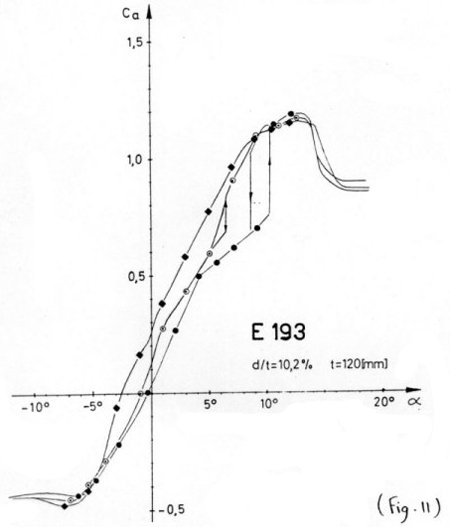
Par contre, dans le cas de l'Eppler 193 (Fig.11), les comportements
de Cz quand a varie dépendent plus sensiblement
du nombre de Reynolds Þ il y a plusieurs
angles de portance nulle suivant le Re !!
De plus, on peut remarquer un phénomène d'hystérésis
sur la polaire tracée avec des points ·.
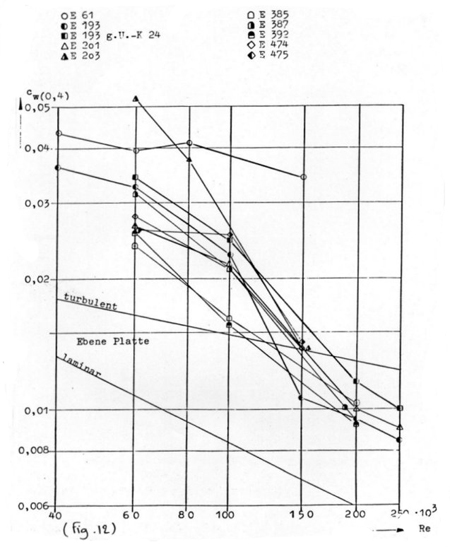
Courbes Cx (0,4) fonction de Re :
Ces courbes ont pour but de comparer les profils entre eux avec d'autres
critères que des critères extrêmes (finesse maxi, vitesse
de chute mini...). Ici, on fixe le Cx = 0,4 et on étudie la variation
du Cz qui lui correspond pour chaque profil en fonction de Re (cf Fig.12).
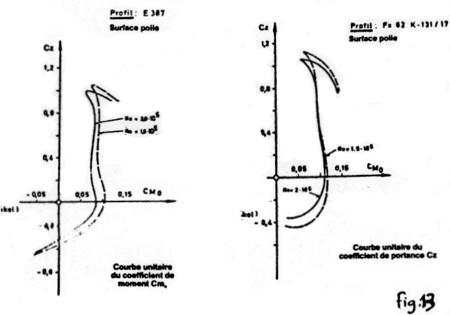
Courbes Cz fonction de Cmo :
Elles sont utiles pour effectuer un calage optimal de l'aile sur le
fuselage et un centrage correct du planeur. en effet, pour la plupart des
formules qui font intervenir Cmo, on considère
ce dernier comme constant.
Il l'est dans la mesure où on vole entre le décrochage
(ou le point de portance maxi) et les Cz négatifs. Par contre, il
varie avec le nombre de Reynolds et on ne peut alors plus le considérer
comme constant; il faut des courbes telles que la (Fig.13) pour le déterminer.
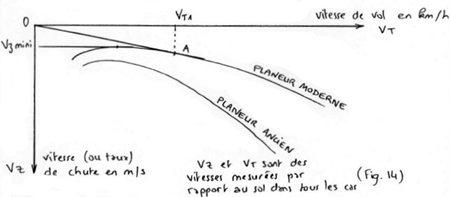
La polaire des vitesses :
elle représente les performances du planeur à différentes
vitesses de vol.
Elle exprime la valeur de Vz (vitesse verticale) en fonction de la
vitesse de vol (vitesse sur trajectoire).
(cf Fig.14) .
Points caractéristiques :
-
Le point de finesse maxi en air calme :
Si l'air n'est animé d'aucun mouvement (pas d'ascendance, de vent...),
la finesse par rapport à la masse d'air qui entoure le planeur est
la même que la finesse par rapport au sol (elle s'exprime par le
rapport
ou encore par les rapports
du planeur, ou
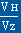
, VH étant la vitesse horizontale et Vz la vitesse verticale.
Si, sur la polaire de la (Fig.14) on mène la tangente passant
par l'origine, on obtient le rapport (
)
maxi,
où VT est la vitesse sur trajectoire; en fait, surtout sur les vrais
planeurs, on néglige l'erreur faite en considérant que le
rapport (
)
maxi
donne la finesse maxi, alors qu'il faudrait considérer le rapport
(
)
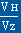
maxi.
On prendra donc A comme point représentant la finesse maxi
et c'est lui qui nous fournira les valeurs de Vz, VT
»VH
correspondant au vol à finesse maxi du planeur.
-
Le point de taux de chute mini :
On trace une tangente horizontale à la polaire et on obtient
Vz mini, la vitesse de chute minimale; ce point est utilisé par
le pilote lorsque, volant en air calme, il veut prolonger son vol le plus
longtemps possible.
Détermination de ces points lorsque le planeur traverse
une masse d'air animée d'un mouvement vertical :
On veut donc déterminer les caractéristiques du planeur
par rapport au sol.
Si le planeur traverse une zone descendante ou l'air chute uniformément
à 2 m/s; toutes les vitesses de chute du planeur par rapport au
sol sont à augmenter de 2 m/s; il faut donc tracer une polaire décalée
de 2 m/s vers le bas (Fig.15).
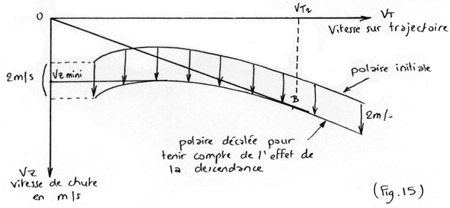
On peut alors déterminer la nouvelle finesse maxi (point B) et
la nouvelle vitesse de chute mini (Vz mini) en menant respectivement une
tangente à la courbe issue de l'origine et une tangente horizontale.
En fait, décaler la polaire de 2 m/s vers le bas revient au
même que de décaler l'origine de 2 m/s vers le haut (cf Fig.16).
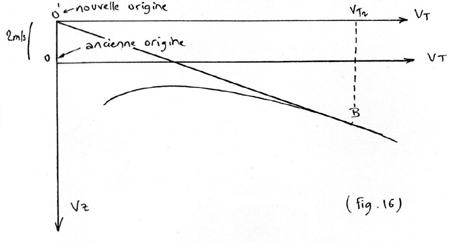
En conclusion: dans une masse d'air descendante vous devez volez
plus vite pour garder la meilleure finesse possible (on voit en effet que
la vitesse sur trajectoire VT2 permettant d'obtenir la finesse
maximale pour un planeur traversant une masse d'air descendante est supérieure
à VT1 trouvée dans des conditions d'air calme).
Il est cependant évident que cette finesse est fortement diminuée.
Remarque: dans une ascendance, si on la traverse en ligne
droite, on a intérêt à voler à Vz mini pour
que le taux de chute du planeur soit le plus faible possible.
Détermination de la finesse maxi par rapport au sol d'un
planeur subissant du vent:
Si le planeur vole avec un vent de face de 30 km/h, il faudra déduire
30 km/h des vitesses de vol.
En reprenant le raisonnement tenu pour les mouvements d'air verticaux,
il faudrait tracer une polaire décalée de 30 km/h vers la
gauche ou décaler l'origine de 30 km/h vers la droite (cf Fig.17).
La finesse maxi sans vent est représentée par le point
A qui correspond à la vitesse sur trajectoire VT1.
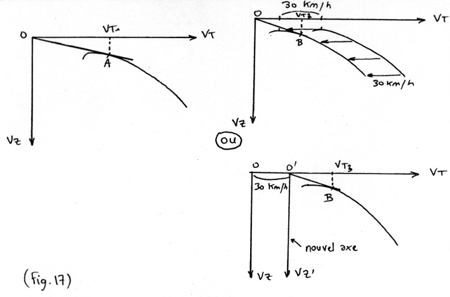
La finesse maxi avec vent de 30 km/h de face a diminué et la
vitesse sur trajectoire par rapport au sol également.
Conclusion : quand le planeur se dirige vers un point du sol
avec vent de face, il faut voler plus vite (par rapport à la masse
d'air) pour garder la meilleure finesse par rapport au sol possible. Il
est cependant évident que cette finesse est fortement diminuée.
Remarque: à partir de la polaire Cx, Cz du planeur et
de la formule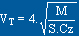 
où M est la masse du planeur en kg et S sa surface alaire en dm²,
VT, la vitesse sur trajectoire en m/s, on peut tracer la polaire
du planeur en Vi, Vz qui permettra de connaître ses performances
et les réglages à lui appliquer selon le vent.
